Пронумеруем комнаты по кругу от 1 до 44 (см рис.).

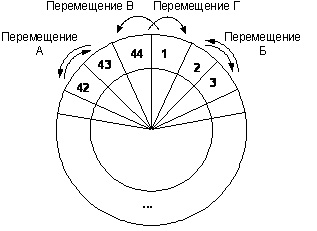
Рис. Комнаты и перемещения документов

Сумма номеров комнат, где располагаются документы, либо не меняется (перемещения А, Б), либо уменьшается на 44 (перемещение Г), либо увеличивается на 44 (перемещение В). Тем самым остаток от деления этой суммы номеров на 44 не меняется. Изначально этот остаток равен 22, поскольку сумма номеров комнат – это сумма элементов арифметической прогрессии, которая равна (общая формула S_n = n*a₁+(n-1)nd/2, где n – число последовательности, a₁ – первый элемент последовательности, d – разность арифметической прогрессии)

S₄₄ = 44 * 1 + (44 – 1) * 44 * 1 / 2 = 990,

990 mod 44 = 22.

Если все документы будут перемещены в одну комнату, то он будет равен 0, т.е. сумма номера комнаты N по числу документов составит N * 44 и (N * 44) mod 44 = 0.

Поскольку от пути перемещения документов, как мы логически рассудили, остаток от деления меняться не должен, то это позволяет сделать заключение, что все документы не смогут быть перемещены в одну комнату.